Статистическая значимость при анализе данных

Что такое статистическая значимость

В процессе любого исследования стоит задача выявить связи между переменными, которые, как правило, характеризуются направлением, силой и надежностью. Чем выше вероятность повторного обнаружения связи, тем она надежнее.

Для проверки гипотез при проведении различных тестов применяется методика статистического анализа. Результатом оценки уровня надежности связи и проверки гипотезы выступает статистическая значимость (statistical significance). Чем меньше вероятность, тем надежнее будет связь.

Аналитик делает такое заключение, используя метод статистической проверки гипотез. По итогам теста определяется p-значения или значение уровня значимости. Чем оно меньше, тем больше будет статистическая значимость.

Обратите внимание! Слово «значимость» в данном контексте отличается по смыслу от общепринятого. Статистически значимые значения не обязательно являются значимыми или важными. Если же уровень значимости низкий, это не говорит о том, что итоги эксперимента не имеют ценности на практике.

Говоря о статистической значимости, стоит иметь ввиду:

• уровень значимости дает понять, что связь между переменными не случайна;
• уровень значимости в статистике может служить доказательством правдоподобности нулевой гипотезы;
• в ходе проверки получаем информацию о том, что результат эксперимента является или не является статистически значимым.

Значимость статистического критерия применяют при испытаниях вакцин, эффекта новых лекарственных препаратов, изучении болезней, а также при определении, насколько успешна и эффективна работа компании, при A/B тестировании сайтов в маркетинге, а также в различных областях науки, психологии.

История понятия уровня значимости

Статистика помогает решать задачи в различных сферах много веков, однако о статистической значимости заговорили лишь в начале XX столетия. Ввел это понятие в 1925 году британский генетик и статистик сэр Рональд Фишер, который работал над методикой проверки гипотез.

В процессе анализа любого процесса есть вероятность, что произойдут те или иные явления. Итоги эксперимента, которые имели высокую вероятность стать действительными, Фишер описывал словом «значимость» (в переводе с английского significance).

Если данные были недостаточно конкретные для проверки, возникала проблема нулевой гипотезы. Для таких систем в качестве удобной для отклонения нулевой гипотезы выборки исследователем было предложено считать вероятность событий как 5%.

Как оценить статистическую значимость

Для проверки гипотезы используют статистический анализ, при этом уровень значимости определяется с помощью p-значения. Последнее показывает вероятность события, если предположить, что определенная нулевая гипотеза верна.

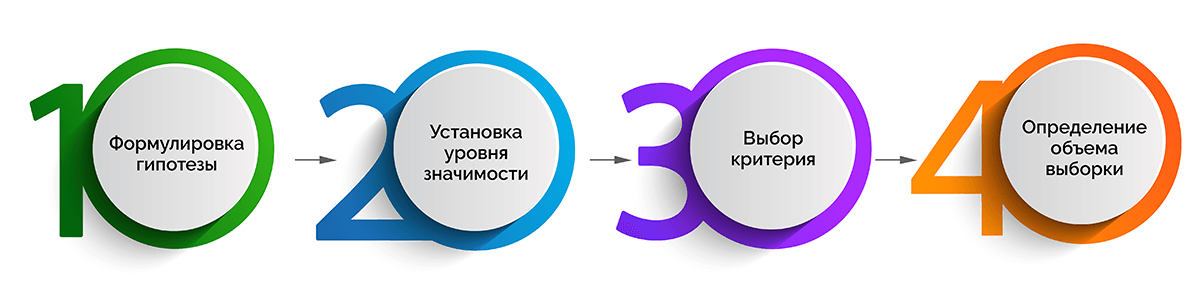
Весь процесс оценивания уровня значимости можно разделить на 3 стадии, которые, в свою очередь, включают следующие промежуточные этапы.

Постановка эксперимента

1. Формулировка гипотезы.
2. Установка уровня значимости, который поможет определить отклонение в распределении данных для идентификации значимого результата.

Если р-значение меньше или равно уровню значимости, данные можно считать статистически значимыми.

3. Выбор критерия – одностороннего или двустороннего.
   Первый подходит для случаев, когда известно, в какую сторону от нормального значения могут отклониться данные. Второй критерий лучше выбирать, если трудно понять возможное направление отклонения данных от контрольной группы значений.
4. Определение объема выборки с использованием статистической мощности. Она показывает вероятность того, что при заданной выборке будет получен именно ожидаемый результат. Зачастую пороговая (критическая) цифра мощности – 80%.

Вычисление стандартного отклонения

1. Расчет стандартного отклонения, которое показывает величину разброса данных на заданной выборке.
2. Поиск среднего значения в каждой исследуемой группе. Для этого осуществляют сложение всех значений, а сумму делят на их количество.
3. Определение стандартного отклонения (x_i – µ). Разница вычисляется путем вычитания каждого полученного значения из средней величины.
4. Возведение полученных величин в квадрат и их суммирование. На данном этапе все числа со знаком «минус» должны исчезнуть.
5. Деление суммы на общий объем выборки минус 1. Единица – это генеральная совокупность, которая не учитывается в расчете.
6. Извлечение корня квадратного.

Определение значимости

1. Определение дисперсии между двумя группами данных по формуле:
   

   

   s_d = √((s₁/N₁) + (s₂/N₂))

   где:
   s₁ – стандартной отклонение в первой группе;
   s₂ – стандартное отклонение во второй группе;
   N₁ – объем выборки в первой группе;
   N₂ – объем выборки во 2-й группе.
2. Поиск t-оценки данных. С ее помощью можно переводить данные в такую форму, которая позволит использовать их в сравнении с другими значениями. T-оценка рассчитывается по формуле:
   

   

   t = (µ₁ – µ₂)/s_d

   где:
   µ₁ – среднее значение для 1-й группы;
   µ₂ – среднее значение для 2-й группы;
   s_d – дисперсия между двумя группами.
3. Определение степени свободы выборки. Для этого объемы двух выборок складывают и вычитают 2.
4. Оценка значимости. Ее осуществляют по таблице значений t-критерия (критерия Стьюдента).
5. Повышение уверенности в достоверности выводов путем проведения дальнейшего исследования.

Статистическая значимость и гипотезы

Гипотеза – это теория, предположение. Если требуется проверка гипотез, всегда используется статистическая значимость. Предположение же называется гипотезой до тех пор, пока это утверждение не будет опровергнуто или доказано.

Гипотезы бывают двух типов:

• нулевая гипотеза – теория, не требующая доказательств. Согласно нее, при внесении изменений ничего не произойдет, т. е. стоит задача не доказать это, а опровергнуть;
• альтернативная гипотеза (исследовательская) – теория, в пользу которой нужно отклонить нулевую гипотезу, т. е. предстоит доказать, что одно решение лучше другого.

Рассмотрим, как статистическая значимость влияет на подтверждение или опровержение альтернативной гипотезы на простом примере.

У компании запущена реклама, которая стала давать меньше конверсий и продаж, чем месяц назад. По мнению маркетолога, причина кроется в рекламных креативах, которые приелись аудитории и требуют замены. Специалист предлагает заменить текстовый материал объявления. Гипотеза состоит в том, что после внесенных изменений будет достигнута главная цель эксперимента: клиенты, пришедшие на сайт с рекламы, станут покупать больше. Теперь маркетологу нужно проводить A/B тестирование обоих креативов, чтобы выяснить, какой текст объявления лучше работает. При высоком уровне достоверности данные условия позволят учитывать результаты такого тестирования.

Проверка статистических гипотез

В случаях, когда информация говорит о незначительных изменениях в сравнении с предыдущими значениями, требуется проверка гипотез. Она позволяет определить, действительно ли происходят изменения или это всего лишь результат неточности измерений.

Для этого принимают или отвергают нулевую гипотезу. Задача решается на основании соотношения p-уровня (общей статистической значимости) и α (уровня значимости).

• p-уровень < α – нулевая гипотеза отвергается;
• p-уровень > α – нулевая гипотеза принимается.

Чем меньше значение p-уровня, тем больше шансов, что тестовая статистика актуальна.

Критерии оценки

Уровень значимости для определения степени правдивости полученных результатов обычно устанавливается на отметке 0,05. Таким образом, интервал вероятности между разными вариантами составляет 5%.

После этого необходимо найти подходящий критерий, по которому будут оцениваться выдвинутые гипотезы: односторонний или двусторонний. Для этого применяют разные методы расчета:

• t-критерий Стьюдента;
• u-критерий Манна-Уитни;
• w-критерий Уилкоксона;
• критерий хи-квадрата Пирсона.

T-критерий Стьюдента

предполагает сравнение данных по двум вариантам исследования и позволяет делать выводы о том, по каким параметрам они отличаются. Метод актуален, когда есть сомнения, что данные располагаются ниже или выше относительно нормального распределения.

Установить, все ли данные лежат в заданном пределе, можно с помощью специальной таблицы значений. Но чаще применяют автоматический расчет t-критерия Стьюдента. Существует много калькуляторов, которые работают по схожему принципу:

1. Указываем вид расчета (связанные выборки или несвязанные).
2. Вносим данные о первой выборке в первую колонку, о второй – во вторую. В одну строку вписываем одно значение, без пропусков и пробелов. Для отделения дробной части от основной используется точка.
3. После заполнения обеих колонок, нажимаем кнопку запуска.

Преимущество коэффициента Стьюдента в том, что он применим для любой сферы деятельности, поэтому является самым популярным и используется на практике чаще всего.

Критерий Манна-Уитни

Рассчитывается по иному алгоритму, но предполагает использование аналогичных исходных данных. Его также зачастую рассчитывают онлайн с помощью специальных сервисов.

При расчете критерия Манна-Уитни есть особенности. Показатель применим для малых выборок или выборок с большими выбросами данных. Чем меньше совпадающих значений в выборках, тем корректнее будет работать критерий.

W-критерий Уилкоксона

Непараметрический аналог t-критерия Стьюдента для сравнения показателей до и после эксперимента, основанный на рангах. Его принцип заключается в том, что для каждого участника определяется величина изменения признака. Затем все значения упорядочиваются по абсолютной величине, рангам присваивается знак изменения, после чего «знаковые ранги» суммируются. Данный критерий применяется в медицинской статистике для сравнения показателей пациентов до лечения и после его завершения.

Критерий хи-квадрата Пирсона

Еще один непараметрический метод для оценки уровня значимости двух и более относительных показателей. Применяется для анализа таблиц сопряженности, в которых приведены данные о частотах различных исходов с учетом фактора риска.

Проблема множественного тестирования гипотез

Если сравнивать группы по различным срезам аудитории или метрикам, может возникать проблема множественного тестирования. Дело в том, что учесть абсолютно все проверки достаточно сложно. Это связано со сложностью предварительного прогнозирования их количества. К тому же, зачастую они всё равно не независимы.

Не существует универсального рецепта решения проблемы множественного тестирования гипотез. Аналитики рекомендуют руководствоваться здравым смыслом. Если протестировать много срезов по различным метрикам, любое исследование может показать якобы значимый для статистики результат. Это означает, итоги тестирования следует читать и интерпретировать с осторожностью.

Вычисление объема выборки и стандартного отклонения

После вычисления критерия оценки (критерия Стьюдента или Манна-Уитни) можно определить, какого оптимального объема должна быть выборка. При этом условии должно быть достаточное для признания достоверности результатов исследования количество людей в фокус-группах, на которых будут проверяться разные варианты.

Недостаточное количество участников эксперимента может стать причиной нехватки выборочных данных для того, чтобы сделать статистически значимый вывод и привести к повышению риска получения случайных результатов.

Объем выборки определяют с помощью статистической мощности (распространенный порог находится на уровне 80%). Этот показатель рассчитывают обычно с помощью специального калькулятора.

Затем можно переходить к вычислению уровня стандартного отклонения, по которому можно узнать величину разброса данных. Его рассчитывают по формуле:

Для упрощения расчетов также используют онлайн-калькуляторы.

Значение p-уровня

Имея две гипотезы – нулевую и альтернативную, необходимо доказать одну из них (истинную) и опровергнуть другую (ложную).

Для этого основатель теории статистической значимости доктор Рональд Фишер создал определитель, с помощью которого можно было оценить, был эксперимент удачным или нет. Такой определитель получил название индекс достоверности или p-уровень (p-value).

P-уровень или уровень статистической значимости результатов – это показатель, который находится в обратной зависимости от истинного результата и отражает вероятность его ошибочной интерпретации.

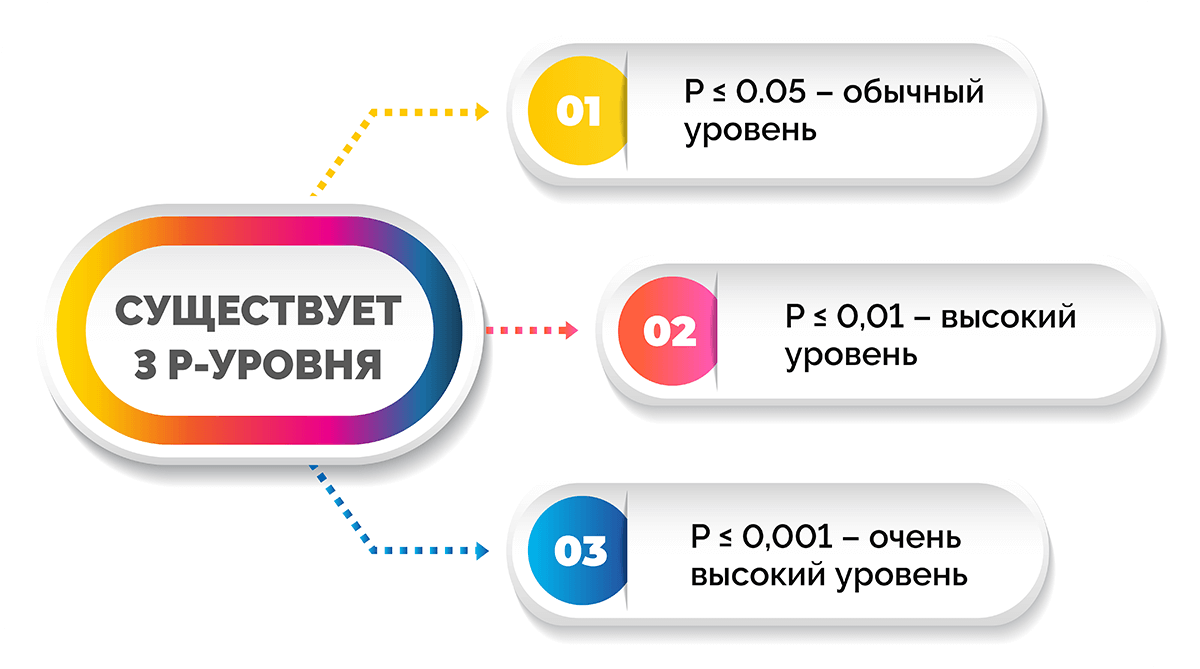
Существует 3 p-уровня.

• P ≤ 0,05 – обычный уровень, т. е. получен статистически значимый результат.
• P ≤ 0,01 – высокий уровень, т. е. выявлена выраженная закономерность.
• P ≤ 0,001 – очень высокий уровень.

Есть и другие значения статистической значимости. Например, уровень p ≥ 0,1 свидетельствует о том, что итог эксперимента не является статистически значимым.

Приближенные к статистически значимым результаты с уровнями p = 0,06 ÷ 0,09 говорят о том, что есть тенденция к существованию искомой закономерности.

Говоря проще, чем ниже значение p-уровня, тем более статистически значимым будет результат эксперимента и тем ниже вероятность ошибки.

Расчет статистической значимости

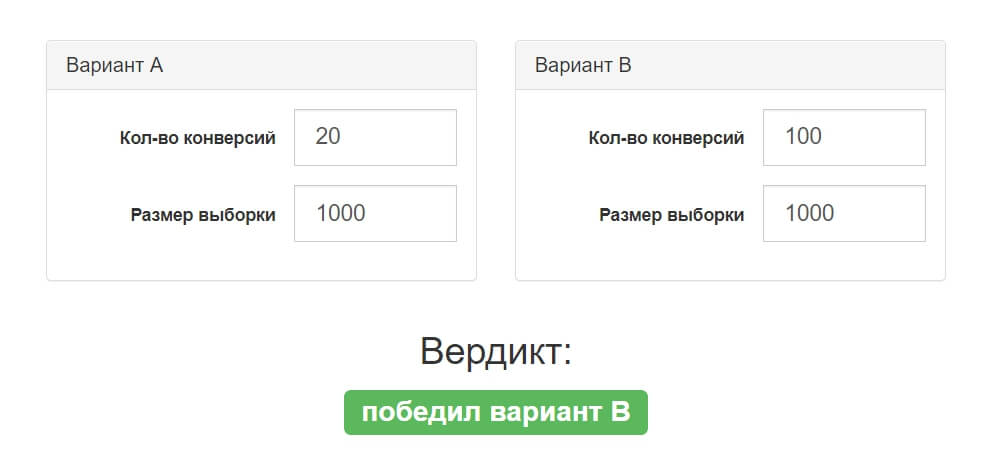
Выше в статье мы рассматривали порядок оценки уровня статистической значимости. Что касается расчета, то вручную он выполняется редко. Большинство аналитиков определяют уровень значимости с помощью онлайн-калькулятора.

В анализе участвуют две гипотезы, для каждой из которых необходимо задать количество конверсий и размер выборки. Сервис автоматически рассчитывает показатель и определяет уровень значимости результата.

Порог вероятности

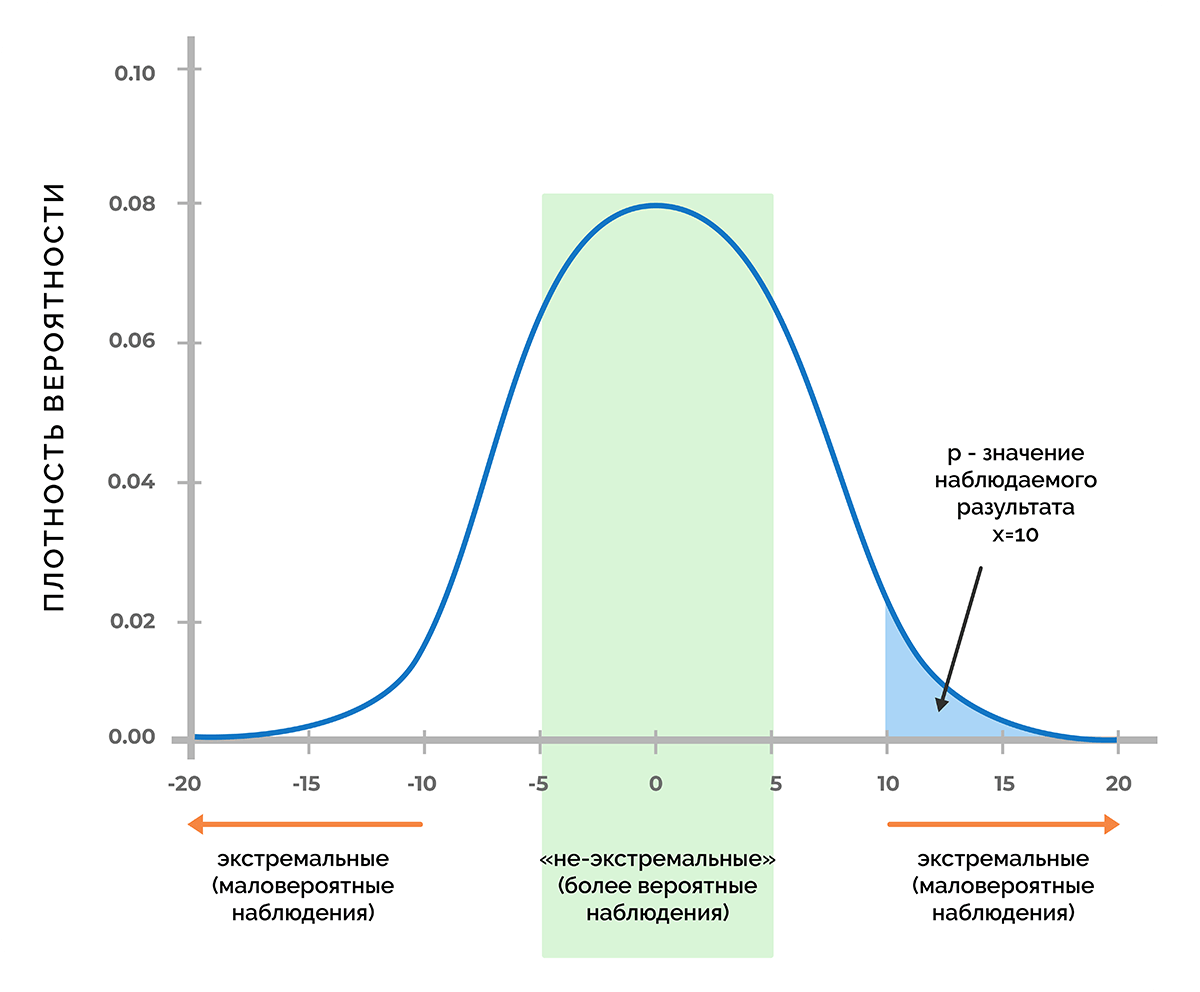
Основа статистической значимости – это вероятность получения нужного значения, если принять как факт, что нулевая гипотеза верна. Если предположить, что в процессе эксперимента было получено некое число Х, то при помощи функции плотности вероятности можно узнать, будет ли вероятность получить значение Х или любое другое значение с меньшей вероятностью, чем Х.

На рисунке изображена кривая Гаусса, соответствующая функции плотности вероятности, которая отвечает распределению значений показателя, при котором верна нулевая гипотеза.

При достаточно низком значении p-уровня не имеет смысла продолжать считать, что переменные не связаны друг с другом. Это позволяет отвергнуть нулевую гипотезу и принять факт того, что связь существует.

Пороги значимости в разных областях могут значительно отличаться. Так, при исследовании вероятности существования бозона Хиггса p-значение равно 1/3,5 млн, в сфере исследования геномов его уровень может достигать 5×10^-8.

Статистическая значимость в A/B тестах

Одной из сфер широкого применения статистической значимости является маркетинг. Аналитики используют исследования для поиска оптимальных путей развития бизнеса, интернет-маркетологи оценивают эффективность рекламных кампаний и посещаемость ресурсов.

A/B тестирование – самый распространенный способ оптимизации страниц сайтов. Его результат невозможно предугадать, можно лишь строить алгоритм работы так, чтобы в конце тестирования получить максимальное количество данных, которые позволят сделать вывод о самом удачном варианте.

Важно, чтобы A/B тестирование длилось минимум 7 дней. Это позволит учесть колебания уровней конверсии и других показателей в разные дни.

Процедура A/B тестирования кажется довольно простой:

1. Создается две веб-страницы (оригинальная и новая).
2. Трафик делится между двумя версиями веб-страницы случайным образом.
3. Собираются данные о каждой версии страницы.
4. Данные анализируются и выбирается вариант с лучшими показателями, а второй отключается.

Важно, чтобы тестирование было достоверным, в противном случае неверное решение может привести к негативным последствиям для сайта.

В данном случае гипотезой считается достижение нужной достоверности. Сама достоверность будет статистической значимостью. Для тестирования гипотезы нужно сформулировать нулевую гипотезу и оценить возможность ее отклонения из-за малой вероятности.

Возможные ошибки

На этапе оценки результатов тестирования можно допустить два типа ошибок:

• ошибка первого рода (type I error) – ложноположительный итог, когда кажется, что различия между показателями двух тестируемых страниц есть, на самом же деле их нет;
• ошибка второго рода (type II error) – ложноотрицательный итог, когда существенная разница между тестируемыми страницами не заметна, но на самом деле она есть, при этом в тестировании видимое ее отсутствие является случайностью.

Как избежать ошибок

Избежать обоих типов ошибок можно, устанавливая при тестировании правильный размер выборки. Чтобы его определить, предстоит в настройках теста задать несколько параметров.

• Чтобы исключить ложноположительные результаты, понадобится указать уровень значимости. Обычно задают значение 0,05, которое будет гарантировать достоверность, превышающую 95%.
• Чтобы избежать ложноотрицательных результатов потребуется минимальная разница в ответах и вероятность обнаружить эту разницу, т. е. статистическая мощность. Последнюю по умолчанию устанавливают на уровне 80%.

Этого достаточно, чтобы вычислить требуемый размер выборки. Обычно расчеты проводятся с помощью спец. калькуляторов.

Можно ли доверять результатам на 100%

К сожалению, даже при правильно проведенной проверке гипотез могут быть допущены ошибки. Это связано с человеческим фактором, а точнее – со скрытыми предположениями, которые зачастую не имеют ничего общего с реальностью.

Вот распространенные предположения, которые приводят к ошибкам:

• посетители сайта, которые просматривают разные варианты веб-страницы, не связаны друг с другом;
• для всех посетителей вероятность конверсии одинакова;
• показатели, которые измеряются в процессе тестирования, имеют нормальное распределение.

На что обратить внимание

Без A/B теста сложно представить развитие современного интернет-продукта. Однако, несмотря на кажущийся простым инструмент, специалисты порой на практике встречаются с подводными камнями. Если знать о них заранее, можно повысить точность тестирования.

Первый узкий момент – проблема подглядывания. Наблюдение за итогами тестирования в реальном времени выступает в качестве соблазна для активных действий, предпринимаемых раньше времени. Обработка «сырых» данных неизменно приводит к статистической погрешности. Чем чаще смотреть на промежуточные результаты A/B теста, тем больше вероятность обнаружить разницу, которой в действительности нет:

• 2 подглядывания с желанием завершить тестирование повышают p-значение в 2 раза;
• 5 подглядывания – в 3,2 раза;
• 10 000 подглядываний – в 12 раз и более.

Решить проблему подглядывания можно тремя способами:

1. Заблаговременно фиксировать размер выборки и не смотреть итоги теста до его окончания.
2. С помощью математических методов: комбинация Sequential experiment design и байесовского подхода к A/B-тесту.
3. С помощью продуктового метода, который предполагает предварительную оценку размера выборки, обеспечивающего эффективность тестирования, и принятие во внимание природы проблемы подглядывания в процессе промежуточных проверок.

Еще один подводный камень заключается в том, что от выигравшей гипотезы ожидают слишком многого. На самом деле в долгосрочной перспективе показатели победителя могут быть менее выдающимися, чем те, которые выдал тест.

Пример статистической значимости

Предположим, разработчики онлайн-игры тестируют два дизайна интерфейса. При A/B тестировании было привлечено 2000 новых игроков: по 1000 пользователей в каждую версию.

В первый день тестирования первая версия дизайна получила 370 возвратов пользователей, вторая – 510.

Как видно, вторая версия дизайна показала лучший результат возвратов. Но разработчики не были уверены, действительно ли это произошло из-за изменения продукта, а не стало следствием случайной погрешности.

Чтобы выяснить это, было принято решение рассчитать уровень значимости для наблюдаемой разницы. Поскольку метрика является простой, можно воспользоваться онлайн-сервисом и вычислить статистическую значимость автоматически.

P-значение < 0,001 в нашем примере свидетельствует о том, что при одинаковых тестовых группах вероятность увидеть наблюдаемую разницу чрезвычайно мала. Это говорит о том, что рост возвратов в первый день с высокой долей вероятности зависит от изменений продукта.

Часто задаваемые вопросы

Заключение

Статистическая значимость является важным методом в ходе проведения экспериментов и исследований несмотря на риск ее неправильной интерпретации. При грамотном подходе погрешность можно свести к минимуму, используя значение в целях повышения достоверности результатов.